The Xeno Arrow Paradox

I think I'm becoming a nerd. Believe it or not, I found yesterday's tutorial on Media Audiences rather interesting. Having said that, I won't be in the least surprised that I might have moved up the Nerd-O-Meter from "Dude with Nerdy Tendencies" to "Nerd with Social Life". Give me two more months and I'll be upgraded to "Nerd with remnants of Social Life", and finally by the end of this semester, I'll just be a full-fledged "Nerd". Still, there is a glimmer of hope, because the most interesting part of the tutorial had little relation to the actual topic at hand.

Our tutor talked about the Paradox of Xeno's Arrow. Now Xeno was this Greek philosopher-mathematician who probably, like every one else during those days, had too much sodding free time on their hands. In order to properly expound this theory, I would require the use of diagrams.


Fig 1.1

Okay, let's introduce you to our two friends (Fig 1.1). Seeing as how this theory was conceptualized during the Greeco-Roman era, we shall use names more suited for that timeframe.


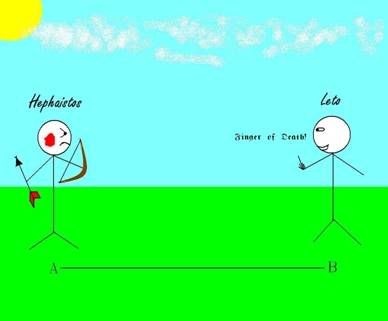
Fig 1.2

So we have Hephaistos the archer and Leto the um... other guy. So they're standing on this little grassy plain on a nice sunny day, minding their own business. Don't ask how they got there and why they're staring at each other like that. This is hypothetical. So everything is cool until Leto the um... other guy gives Hephaistos the archer the Finger (Fig 1.2).


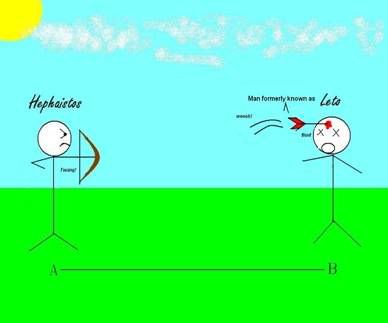
Fig 1.3

Hephaistos the archer naturally gets angry. And back in those days where feudalism was more openly received and less questioned, it was perfectly okay for Hephaistos the archer to shoot Leto the other guy in the head (Fig 1.3). Very commonplace incident in ancient Greece; the people learn that Hephaistos the archer is one violent bugger so keep away from him, the people learn that Leto the other guy is dead - wouldn't you know, that son of a bitch still owes us fifty denarii! - and then they go on drinking their beers. Nothing specially, really.

But here's where Xeno comes in; it gets a tad mathematical now, so if your standard of Additional Mathematics plateaus at problems like "If I have two apples, how many apples do I have?" (Fig 1.4) then I'd suggest not going further until you've rectified that. Now Xeno theorizes that before the arrow can reach Point B from Point A, it has to pass the midpoint M (Fig 1.5).


Fig 1.4


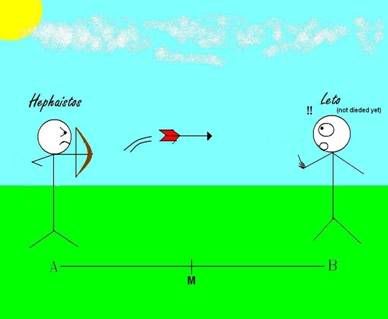
Fig 1.5

Sounds okay so far? Now as if that weren't enough, Xeno goes on to say that before the arrow reaches M, it has to first reach the midpoint between A and M, Midpoint N (Fig 1.6).


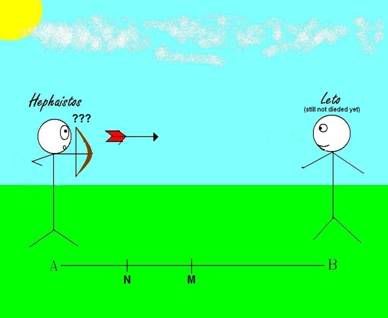
Fig 1.6

Now that's just fine and dandy. Sure, it makes sense. Before you get to the midpoint, you need to get the midpoint of the midpoint. Whatever. End of story right? Wrong-O, because Xeno now says that in order for the arrow to reach N, it has to first reach the midpoint between A and N, Midpoint O (Fig 1.7).


Fig 1.7

Yes, you've guessed it, in between A and O, there is another midpoint in which the arrow must first traverse, in between which, there is yet another midpoint. So Xeno theorizes that since there is no finite number of the divisions of midpoints (i.e. any number can be divided by half, no matter how small), there will be no end to the midpoints that the stupid arrow must first reach. And therefore, if you fire an arrow, the arrow will never reach point B (Fig 1.8).


Fig 1.8

And that is the paradox of Xeno's Arrow. Really interesting if you think about it, that this Greek Xeno actually had the audacity to come up with such a bold theory that defies the laws of Physics. Either he must have been a mathematical genius, or he just wanted to find a way to deter people from constantly shooting arrows at him.

So if you're at a rave party and are called upon to make small talk, show them that you too could be a nerd/geek/wanker (delete wherever appropriate, if deletion is appropriate to begin with) and share with them the Xeno's Arrow Paradox. It sure beats constantly commenting on how huge that chick's rack is at any rate. Besides, it's also a great time to show the girls some of your pseudo-intelligence (Fig 1.9)


Fig 1.9

And so ends my lengthy discourse of the Xeno's Arrow Paradox. For what it's worth, I have a funny feeling that Xeno might have at one point realized that there was a serious flaw in his little theory. But as it turned out, I don't think he was around for too long to find out what it was (Fig 1.10)


Fig 1.10

THE END!

The Monash Blues

I wasn't able to sleep last night. So aside from thinking about that special someone whom I care for so much about, I picked up the guitar and started strumming some 6/8 blues chord progressions.

The cool thing about blues is that it complains about anything and everything in general. And what better thing to complain about than our beloved Monash Malaysia, the campus we (as in all those who are in it) all love to hate. In a matter of minutes, the lyrics started flowing in. Enjoy!

Disclaimer: The following might offend some people, especially those who have a dim sense of humour. And if you are offended, then this post has served its purpose, because to cut a long story short, it's probably most likely that you are one of those wankers whom I'm talking about. Learn to laugh at yourself, because if not I'll do the laughing for you, and everyone else for that matter.

The Monash Blues
by Eddie G.

This morning I was late for class
But the security guard wouldn't let me pass
"Where's your Monash ID?" he said
I think the power's getting to his head
I've got the blues
Baby I've got the Monash Blues

I'm sittin' in lectures, starin' at the screen
My eyes are turnin' red and my face is turnin' green
I looked at the lecturer, he looked at me
I worked so hard but all I got was a P
I've got the blues
Baby I've got the Monash Blues

I'm a growin' man; I eat when I could
I guess I'll have me some cafeteria food
The cafe's a prison 'cos the food is like hell
I guess I'll eat up and head back to my cell
I've got the blues
Baby I've got the Monash Blues

I guess I must have had too much to drink
I'll pay a little visit to the toilet I think
But when I got there, you could imagine the scene
"Cleanin' in progress" if you know what I mean
I've got the blues
Baby I've got the Monash Blues

[musical interlude]

I'm headin' to the com lab to print my stuff
There are many computers, but there ain't enough
And there are some fuckers who leave their shit on
They go for a smoke and then *POOF* they're gone
I've got the blues
Baby I've got the Monash Blues

The MUSA Student Lounge is a cool place to be
Until the Sunway College bastards come in for free
They should keep to their side of the school
Instead of playing our foosball and playing our pool
I've got the blues
Baby I've got the Monash Blues

I'm just a poor sod, and that's a fact
The tuition fees have broken my back
And let me tell you somethin' - this ain't funny
The MUSA wankers are wastin' our money
I've got the blues
Baby I've got the Monash Blues

We live in oppresion and organized crime
They've stolen our money and stolen our time
All this red tape really makes me sick
The Sunway Group can suck my lollipop
I've got the blues
Baby I've got the Monash Blues

I've got the blues
Yea I've got the blues
Help me! I've got the blues
Baby I've got the Monash Blueeeeeeeeeeeeeeeees!

[standing ovation; take a bow Eddie G.]

Footnote: See, Lee. It's easy to write lyrics, all you have do is be bored, or can't sleep, or whatever. You get my point. :P Good luck, dear.

Police Story II, Man!

After the overwhelming response I received from the much-acclaimed Police Story, Man! I have decided to start work on its sequel. Plot framework is still in the process of gestation, but the general layout of events are more or less finished. The casting is also more or less sorted out. I don't want to spoil it for my ardent fans, so the roles will be pointed out in general.

Cast: Role

Eddie G.: Same as PSM
Max Tan: Same as PSM
Trudy Au: Same as PSM
Wilson Lee: Same as PSM
Aaron Lee: You'll find out soon enough
Kel Li: Villain role
Carrie Low: Villain role

There are also openings for minor roles, about seven (7) of them. Interested parties please let me know. There is only one pre-requisite for your involvement (besides committing your time and effort in the filming, which is a dead given), and that is you must speak better Cantonese than I do (which is nothing much, really). So give me a buzz. Those who would like to involve themselves in camara-work, please let me know too.

Cheers!

p.s. TMY, I'd like you to keep up your 100% cameo appearance in my shows. I'll be giving you a call soon.

Chloe

By Eddie G.

Chloe sat quietly in her living room, her hands cupped onto her chin. She was waiting eagerly for someone to call, but the phone showed no inclination of complying to her whim. With her elbows resting on her knees, she stared at it with great intensity, almost as if telepathically willing the phone to ring. It did not.

There was a sudden rush of air behind her, but that did not take her vice-like attention away from that phone. Why wasn't he calling? Didn't he realize that she still thought of him with every waking moment of her life?

"Ring, damn you! RING!" she hissed.

"Talking to inanimate objects again, aren't we?" mused a voice from behind her. It was a voice that she was familiar with. And truthfully, it was a voice she also wanted to hear. Although it was not the voice that she had been desperately waiting for at the other end of the telephone, this one would suffice for now.

"What are you doing here, Angel?" she asked without looking back.

Many of her friends believed Angel to be a figment of Chloe's imagination, just like how a 5-year-old would normally have the tendency to make up an imaginary friend. But Chloe was convinced that Angel existed, and that was all that mattered to her. Suspicions arose when, like Batman and Bruce Wayne, Chloe and Angel were never seen together by Chloe's friends before, and yet she would always talk about him. She felt that Angel too, wherever his world may be did the same, and received the same strange looks from his friends.

"I heard your sigh from miles away and decided to come and cheer you up," Angel declared.

"That's sweet of you, Angel," she sighed, "but I'm afraid even you can't help me now."

Angel sat down on the sofa and put his arm around her.

"Try me," he grinned. It was a grin that always made Chloe smile. And this time was no exception.

"He hardly ever calls me anymore," she lamented, "and all I want is to hear his voice again."

"Oh? And whose fault is this that, pray?"

Chloe pouted. "Look, if you're supposed to be cheering me up, you're doing a sterling job," she said.

"Now, now," coaxed Angel, "before you start pointing your finger at the whole damn cruel world in general, let's take time to reflect on why you think he's not been calling, shall we?"

Chloe chewed her lip briefly. She hated it when Angel made her think like that, but she let her mind work through the possibilities. It was more productive than attempting to apply telekinesis on the telephone anyway.

"I really can't think of a reason why he wouldn't call," she said finally.

"Why don't you call him, then?"

"Because…" she hesitated, "because I'm scared." It was almost a whisper.

Angel merely nodded.

"So you're telling me that… he's scared. But what is he scared of?" she pressed.

"The same thing that you are scared of, my dear."

Suddenly the revelation hit her, and she stood to her feet for the first time in hours. "He's afraid that he might not be able to let go of me!"

Angel remained seated stoically on the sofa, and merely nodded again.

Chloe felt as if a huge weight had been removed from around her ankles. Happily she picked up the phone and began to dial.

"Who are you calling at this hour?" Angel queried, although he already half-knew the answer.

Chloe did not reply him, but merely waited for the line on the other to get through. "Hello?" she said, "yea hi! It's me. I was thinking if you'd like to, you know, go out for some coffee? Um… how about right now? Sounds great! Okay, see you in bit then! Byeee!"

Upon replacing the receiver, she did a happy little spin.

"Alright, Angel. I'm going out now. I'll see you in a bit, yea?" she said.

Angel again merely nodded. It was almost as if his energy and cheer had been transferred to Chloe, and in return he was bearing what once used to be her melancholy.

That was the role of the martyr, he reminded himself, but someone had to carry the burden.

"Have fun, dear," was all he could say.

It was about three hours later when Chloe returned to her apartment. Angel still sat there stoned on her sofa, a bottle of whiskey opened in front of him.

"Hey! I'm back! Guess what? I…" her voice trailed off, "have you been drinking, Angel?"

Angel giggled, clearly inebriated. He looked her in the eye for a good thirty seconds.

"No," he said finally with drunken determination.

Chloe gave a quiet sigh as she tried to remove the bottle away from his hands.

"Leave me alone!" snarled Angel, slapping her hand away angrily.

"What the hell is wrong with you?" she fumed, "are you out of your mind?"

Angel staggered to his feet. "Chloe," he said, placing his hand firmly on her shoulder, "there is… something… I want… to tell you!"

"What?"

"Chloe, I… I…" he hesitated for a while, not knowing what to say. "Chloe, I really..." No, that's not going to work either "Chloe, I..." ah screw it! "I think I may be drunk," he said, and then he passed out on the sofa.

Chloe brought out a couple of blankets from her room, and covered the sleeping Angel. It was most peculiar indeed, this sudden change of behaviour from him. Gently, she knelt beside him and stroked him on the forehead. He was sleeping serenely now, and Chloe felt sure that the even the most tumultuous of tempests would not wake him.

"Goodnight, Angel," she said, and kissed him on the cheek.

She dimmed the lights and headed to her room, closing the door behind her.

Thou Shalt Not Have Any Other Gods Before Me

So it says in the Bible. But imagine how queer life would be like if there were other gods; I'm not talking about Buddha or the Prophet (caricatures while you wait) or the deities of other major religions, but gods of everyday taken-for-granted activities or practices. Seeing as how God Himself has a sense of humour, here are some "gods" He might close one eye to.

Jeff, God of the Queue

Jeff, God of the Queue is an impatient and impetuous deity created by the awareness of irate shoppers and diabolical tollbooth operators. He sits broodingly on his Throne, ensuring that queues all over the world are going the way he wants them to. Loyal worshippers of Jeff are rewarded by somehow finding their queues shorten even before they realize it. On the other hand, those who incur his wrath find themselves waiting as long as eternity can stretch for that bloody old woman (who really shouldn't be in the Express Lane - 10 Items or Less Thank You Very Much - in the first place) to place two months worth of groceries painstakingly on the counter, fumble in her purse to find her son's credit card, hem and haw when she realizes she left it at home, place all her groceries back into the trolley and wheel them back. All this while the adjacent lane zips casually by.

The thing that gets under Jeff's skin the most is how mortals foolishly misinterpret his deified role. Nothing miffs the Queue God more than aspiring pool/snooker players beseeching Jeff to bless their game instruments. They of course are punished for their blatant ignorance, not while they are playing - that would be too lenient - but when they decide to pay a visit to the lavoratory.

Ravioli, the God of Pasta

Revered by chefs all over Italy, Ravioli's favour is hard-sought and even harder-earned. Many Italian chefs have wasted their youths just so that they could gain the patronage of the Pasta God and the inspired recipes that he bestows. Those who have found enlightenment, though, will readily tell you that it was truly worth the wait, for there is nothing more possibly gratifying than a nice hot plate of mushroom cabonara served with a side of garlic bread (Fuck, I just made myself hungry).

Ravioli sits on his Throne somewhere in the skies of Italy. While some believe it to be situated above Naples, there are those who argue that the Pasta God can reside nowhere else but above their beloved capital, Rome (much to the indignance of the non-conformists). While, until today, the whereabouts of Ravioli's Throne remain a great mystery, his prophets have assured us that he is NOT in Pisa. The answer is bloody obvious: staring at the Leaning Tower all day is more than enough to give him a splitting headache.

On the left of Ravioli's throne is a long table laid with all kinds and styles of pasta one can ever imagine (and much more). Those who are found worthy of entering this Pasta Heaven will realize that the bowls of mouth-watering pasta will never run out or be lacking. That however, is just Basic Membership. Worshippers who have made it to Gold Membership will find themselves not getting fat no matter how much they consume. And then there are those who are truly One with Ravioli; these privileged few will find that no matter how much they eat, they will never grow fat nor get full.

The space on the right of Ravioli's throne is dedicated to punish those who have maligned the beautiful name of Pasta (impossible as it may sound). Those who can be found here include chefs who use monosodium glutamate in their dishes. Their punishment is to be force-fed with their own MSG-laid pasta for all eternity, with no water source in sight. But a greater punishment awaits those who commit the Unpardonable Sin of commercializing pasta. If it's one thing that the God of Pasta cannot stand, it is the use of pasta to exploit the public. Offenders will have find themselves decapitated, have their heads stuck on a pike and forced to eat their own junk while watching eternal re-runs of their own tasteless television advertisments. Even as we speak, pikes are currently being reserved for the CEOs of MNCs who use pasta to rip off the public like Pizza Hut and, in the near future, MacDonalds.

Eleva, Goddess of the Stairs

When they were up they were up, and when they were down they were down, and when they were only half-way up, Eleva the Stair Goddess came around and shoved their indecisive asses over the railing. So the next time you plan on taking a flight of stairs for granted, remember all those unfortunate sods that she hurled headlong down while they cursed and grumbled on her turf.

As far as Eleva is concerned, it doesn't matter which God you serve, you still have to get through her heaven (or hell) to reach whatever heaven (or hell) you believe in. Furthermore, those who incur her wrath will soon find out that they'll probably reach there all the earlier. Countless fools have slipped on innocent looking banana peels (which for some strange reason happened to be at that exact spot at that exact time) and tumbled to their demise, sometimes in rather gruesome fashion. Unlike other deities, Eleva does not reward those who are faithful, for she feels that the privilege to walk up and down a flight of stairs safely and unhindered is already a reward in itself.

The Stair Goddess is easily pleased and equally easily angered. To please her, simply traverse her domain quickly, quietly and thankfully. Contrary to popular belief, those who go up one stair at a time saying "All praise to you great Eleva, without whom we are naught" will not earn extra points with her and are probably more liable to get the old "banana peel" routine. Other things that tick Eleva off are people who treat the stairs like Plan B. The one thing she hates the most is the way people always complain how the lifts have broken down and thus they are forced to used to stairs. Eleva's message to such fools is clearly stated in Book of II Ascension, Chapter 4 Verse 6 in the Stairway Bible.

"Foolishe Mortal! Quit thy grumbling, fore thou art not forced to use the stairs when the lifte faileth. Observe Spiderman and Batman, and learne ye well!"
- II Ascension 4:6

Another thing that Eleva frowns terribly upon is how people scale up and down her domain repeatedly for exercise. Her disdain is also recorded in the Stairway Bible.

"How dare ye! that you treat my Holy Domaine as if it were a bloody gymnasiume you fat tub of larde! Get thee hence before I decide to turn thee into a human pushballe!"
- Zepellin 19:8

Surprisingly, Eleva is very lenient to idiot skateboarders who enjoy nothing more than doing grinds down her stair rails. Although her motives are unclear, many of her prophets believe that she lets them off so that she can build up their pitiful egos, only to send them crashing down.

ALL the way down.


More to come in Part II...